有没有大神可以把力矩的物理意义讲清楚？

谢邀，这里从物体(刚体)的转动说起。

如果看得累，可以至少看完第一 、第二部分~

一、物体转动与力矩的关系

首先，物体的运动有平动(Translational Motion)和转动(Rotational Motion)。比如，在斜面上推动一滑块，则该滑块为平动；开门时门绕定轴转，则为该门为转动。

物体平动时有位移 x ，转动时有角位移 \theta ；平动时有速度 v=\frac{dx}{dt} ，转动时有角速度 \omega=\frac{d\theta}{dt} ；平动时有加速度 a=\frac{dv}{dt}=\frac{d^{2}x}{dt^2} ，转动时有角加速度 \alpha=\frac{d\omega}{dt}=\frac{d^2\theta}{dt^2} 。

力(Force)直接改变物体平动状态，力矩(Torque)直接改变物体的转动状态！

合外力是物体平动状态改变的原因，而合外力矩是物体转动状态改变的原因！

对于平动，有 F=ma ，其中 F 为合外力， m 为惯性质量（即质量）， a 为加速度；而对于转动，有 M=J\alpha ，其中 M 为合外力矩， J 为转动惯量， \alpha 为角加速度。

（对于转动也有写法为 \tau=I\alpha ，其中 \tau 为合外力矩， I 为转动惯量， \alpha 为角加速度。）

由此可知，力直接导致物体的加速度，而力矩直接导致物体的角加速度。当然，当合外力矩为0时，物体不转动，比如杠杆平衡。

二、对力矩计算的理解

力矩 是 力的一种使物体以一定角加速转动的能力。

M=r\times F （矢量的叉乘）

力矩的大小： M=r_{\bot}F=rF_{\bot}=rFsin\varphi

力矩的方向：垂直于 r 和 F 所在的平面

三、力矩与物体静平衡

一个物体静平衡，既需要达到平动上的平衡也需要达到转动上的平衡。

平动上的平衡要合外力为零，而转动上的平衡要合外力矩为零。

即静平衡需要： \Sigma F=0 且 \Sigma M=0

这里给一个简单的物体静平衡的例子：

一长度为 l 、质量为 m_1 的梯子倚靠在光滑墙面上，与地面夹角为 \theta 。某工人站在梯子的三分之二高处，其与手上器具的总质量为m_2 。 若墙面与梯子的摩擦忽略不计，为了防止梯子下滑，梯子与地面的静摩擦系数至少要是多少？

梯子不下滑，需要静平衡，则合力、合力矩都必须为0.

受力分析：

F_{Nh} - 墙对梯子的支持力

F_{NG} - 地面对梯子的支持力

F_{f} - 地面与梯子间的摩擦力

F_{gl} - 梯子的重力

F_{gFF} - 人与器具的总重力

选择梯子与地面的接触点为支点：

因为\Sigma F=0，所以 \Sigma F_x=0 且 \Sigma F_y=0 。

首先 \Sigma F_y=0

则 F_{NG}+F_{gl}+F_{gFF}=0

F_{NG}-m_1g-m_2g=0

F_{NG}=(m_1+m_2)g

同时 \Sigma M=0

则有 M_{NG}+M_{f}+M_{gl}+M_{FF}+M_{Nh}=0

0+0+\frac{l}{2}cos\theta m_1g+\frac{2}{3}lcos\theta m_2g+lsin\theta F_{Nh}=0

F_{Nh}=\frac{lcos\theta(\frac{1}{2}m_1g+\frac{2}{3}m_2g)}{lsin\theta} =cot\theta (\frac{1}{2}m_1g+\frac{2}{3}m_2g)

还有 \Sigma F_x=0

则 F_f+F_{Nh}=0

F_f=-F_{Nh}

\left| F_f\right|=\left| F_{Nh}\right|=cot\theta (\frac{1}{2}m_1g+\frac{2}{3}m_2g)

则梯子与地面的静摩擦系数至少为

\mu=\frac{F_f}{F_{NG}}=\frac{cot\theta (\frac{1}{2}m_1g+\frac{2}{3}m_2g)}{(m_1+m_2)g}=\frac{cot\theta (\frac{1}{2}m_1+\frac{2}{3}m_2)}{m_1+m_2}

四、力矩与物体平动加转动

一个物体平动遵守 F=ma， 转动遵守M=J\alpha。

【其中 F 为合外力， m 为惯性质量（即质量）， a 为加速度；M 为合外力矩， J 为转动惯量， \alpha 为角加速度。】

这里给一个简单的物体平动+转动的的例子：

如图，细绳包裹着一个质量为 m ，半径为 R 的均匀实心圆柱体，圆柱体从静止开始下落。该圆柱的转动惯量为 \frac{1}{2}mR^2 。则当圆柱下落时细绳的拉力是多少？

受力分析：

T - 细绳拉力

mg - 圆柱重力

该均匀圆柱绕质心转动，故力矩的大小为 M=TR 。

所以合外力矩为 M=TR 。

由于M=J\alpha

故有 TR=\frac{1}{2}mR^2\alpha ······ (1)

由于F=ma

故有 mg-T=ma ······ (2)

线加速度 a 与角加速度 \alpha 的关系为： a=R\alpha ······ (3)

联立(1)(2)(3)，可得 a=\frac{2}{3}g

将a=\frac{2}{3}g 代入(1)，得当圆柱下落时细绳的拉力为 T=\frac{1}{3}mg 。

五、力矩与角动量

物体的角动量等于其转动惯量与角速度的乘积： L=J\omega ，其中 L 为角动量， J 为转动惯量， \omega 为角速度。

则其微分形式为 dL=Jd\omega

由于 M=J\alpha , \alpha=\frac{d\omega}{dt}

故力矩可重新表示为 M=J\frac{d\omega}{dt}=\frac{dL}{dt}

由此可知，物体所受的外力矩等于其角动量的变化率。

由M=\frac{dL}{dt}，可得 \Delta L=\int_{t_1}^{t_2}Mdt

由此可知，角动量的变化量是力矩对时间的累积效应。 \Delta L 也称为冲量矩。

这可以类比于物体平动所受的外力等于其动量的变化率、物体平动动量的变化量（冲量）是力对时间的累积效应。（F=\frac{dP}{dt} 、 \Delta P=\int_{t_1}^{t_2}Fdt）

六、力矩做功

首先，功的基本定义是：

dW=F\cdot dr

然后如下图：

进一步地，根据矢量的点乘，对于定轴转动物体有 dW=F\cdot dr=(F_{\bot})(r d\varphi)

则 dW=(F_{\bot}r) d\varphi=Md\varphi

故 W=\int_{\varphi_1}^{\varphi_2}Md\varphi

因此，对(定轴)转动物体做的功，是力矩做的功。

类比于物体平动时力做功 W=\int_{r_1}^{r_2}F\cdot dr ，物体转动时有力矩做功 W=\int_{\varphi_1}^{\varphi_2}Md\varphi。

七、力矩与转动动能定理

之前所说外力矩做功有：W=\int_{\varphi_1}^{\varphi_2}Md\varphi

由于 M=J\alpha ， \alpha=\frac{d\omega}{dt}

故有 W=\int_{\varphi_1}^{\varphi_2}J\alpha d\varphi=J\int_{\varphi_1}^{\varphi_2}\frac{d\omega}{dt}d\varphi

由于 \omega=\frac{d\varphi}{dt}

所以 W=J\int_{\omega_1}^{\omega_2}\omega d\omega=\frac{1}{2}J \omega_{2}^{2}-J\omega^2_1

因为定义物体的转动动能为 E_k=\frac{1}{2}J\omega^2 ， 所以 W=E_{k_2}-E_{k_1}。

由此可知，合外力矩对物体做的功等于该物体转动动能的变化量。这就是转动中的动能定理。

这可以类比于物体平动时的动能定理：合外力对物体做的功等于该物体平动动能的变化量。

八、机械能守恒时力矩与势能的关系

在没有非保守力时机械能守恒：

E_{总}=E_k+E_p=常数

其微分形式为

dE_{总}=0=dE_k+dE_p

由于功等于动能的变化量 W=\Delta E_k=E_k-E_{k_0} ，微分形式 dW=dE_k

所以当机械能守恒时势能与功的关系为

dW=dE_k=-dE_p

之前已提， 对于定轴转动物体有 dW=Md\varphi

则 M=\frac{dW}{d\varphi}

故有 M=-\frac{dE_p}{d\varphi}

（注意仅当力矩是由保守力产生时该关系才有效。)

九、力矩与功率的关系

功率的定义为 P=\frac{dW}{dt}

之前已提， 对于定轴转动物体有 dW=Md\varphi

则 P=\frac{dW}{dt}=\frac{Md\varphi}{dt}

由于角速度 \omega=\frac{d\varphi}{dt} ，所以有 P=M\omega

类比于物体平动时功率 P=F\cdot v ，物体转动时有功率 P=M\omega 。

不过其实我写的打的也挺累的，给个赞吧~

啊这

考虑 \vec r \times \vec F

由牛顿第二定律：

\vec r \times \vec F=\vec r \times (\frac{d}{dt}\vec p)

由求导法则：

\vec r \times \vec F=\frac{d}{dt}(\vec r \times \vec p)+\vec p\times \frac{d}{dt}\vec r

而最后一项可以变形成

(m \vec v)\times \vec v=0

因此

\vec r \times \vec F=\frac{d}{dt}(\vec r \times \vec p)

定义 \vec r \times \vec p=\vec L 为系统的角动量，它的其中一个意义是质点矢径扫过面积速度的大小（读者自证），则

\vec r \times \vec F=\frac{d\vec L}{dt}

由此可以看出，力矩实际上对应一个转动上的效果，一如力对应一个平动上的效果

（如果你把上式写成 \vec M=\frac{d\vec L}{dt} ,对比 \vec F=\frac{d\vec p}{dt} ,可以看出 \vec F\rightarrow \vec M , \vec L\rightarrow \vec p ,两者形式上是一样的，因此你可以认为力矩就是转动中的“力”)

而实际上，在刚体力学中，设角速度 \vec \omega ，则

\vec M=\frac{d\vec L}{dt}=\frac{d}{dt}(\int_{}^{}(\vec r\times(dm\times\vec v)))=\frac{d}{dt}(\int_{}^{}(\vec r \times(dm\times(\vec \omega \times \vec r))))

由矢量分析公式：

\vec r \times(\vec \omega \times \vec r)=\vec \omega\cdot(\vec r\cdot\vec r)-\vec r\cdot(\vec \omega \cdot \vec r)=r^2\vec \omega-\vec r\cdot(\vec r \cdot \vec \omega)

代入得

\vec M=\frac{d}{dt}(\int_{}^{}(dm\times(r^2\vec \omega-\vec r\cdot(\vec r \cdot \vec \omega))))

引入惯量张量 \overleftrightarrow{I} , \overleftrightarrow{I}_{ij}^{}=\int_{}^{}(dm \times (r^2\delta_{ij}^{}-\vec r_{i}^{}\cdot\vec r_{j}^{})) ,其中 \delta_{ij}^{} 是克罗内克尔记号，当且仅当 i=j 时等于1，其余时候等于0,则

\vec M=\frac{d}{dt}( \overleftrightarrow{I}\cdot \vec \omega) ,这就是著名的刚体角动量定理，力矩之于转动的效果也可见一斑

以上。

角动量是空间旋转对称性下的守恒量，动量是空间平移对称性下的守恒量。（诺特定理）

力的时间累积效应对应了动量的变化量，力矩的时间累积效应对应了角动量的变化量。

那你就可以理解成力矩对应空间旋转系下物体间的相互作用。

将这个问题分成三步来回答，希望高中生也能理解。

一，为什么需要力矩和角动量的概念。

我们知道力和动量的关系为 Fdt=mdv=dP ，即力的大小决定了动量的变化速度。这适用于物体的平动。

如果我们引入转动，则势必需要考虑物体的受力点和转动轴之间的距离 r （力臂）。我们在上式两侧都乘上力臂，就变成 rFdt=rdP=drP 。我们将 rF 称作力矩（ \tau ），而 rP 称作角动量（ L ），则上式变成 \tau dt=dL ，意味着力矩的大小决定了角动量的变化速度。

二，力矩的方向和角动量的方向

形成力矩的两个量，力和力臂，都是矢量；类似的，形成角动量的两个量，动量和力臂，也都是矢量。因此，力矩和角动量也是矢量。我们可以进一步将这些物理量表示成 {\displaystyle {\vec {\tau}}} 、 {\displaystyle {\vec {L}}} 、 {\displaystyle {\vec {F}}} 、 {\displaystyle {\vec {r}}} 和 {\displaystyle {\vec {P}}} 。矢量相乘是叉乘，满足右手定则。我们可以让力臂的方向箭头穿入手掌，四指朝向力（或动量）的方向，则大拇指指向力矩（或角动量）的方向。

注意，力矩和角动量的方向并不一定相同，力矩的方向指向角动量变化的方向。

三，力矩的大小

如前所述，力和力臂相乘是叉乘。计算力矩的大小时需要将力以平行四边形法则进行分解，只有垂直于力臂的分力才能提供力矩。

所以，我们一般可以用 \left| \tau \right|=\left| r \right|\left| F \right|sin\theta 来计算力矩的大小。

以上。

尝试回答一下这个问题。

一个刚体，比如一块石头m受到一个力F的作用。

按照牛顿第二定律，会产生一个加速度a,做均加速直线运动，F=ma。

力可以理解为 以加速度a运动的质量为m的物体的一种静态的状态描述。

力的大小数值上等于单位质量物体的加速度大小。

对于转动，力矩M=nb(其中n是转动惯量n=mr²,b是转动加速度，r是质点到转动中心的距离)。

力矩可以理解为 以转动加速度b运动的转动惯量为n的物体的一种静态的状态描述。

力矩的大小数值上等于单位转动惯量物体的转动加速度的大小。

他们描述的都是静态的，描述的都是物体所处的一种状态。

只不过，力描述的是直线运动的一种状态。 力矩描述的是转动运动的一种状态。

直线运动和转动在t时刻，在A点重合，所以力矩和力可以通过乘r来换算。M=Fr

手机打字不容易，点个赞在走吧

有些场合下力矩的地位就和力差不多，在转动时会有所谓“力矩做的功”。

力矩对于角动量，就犹如力对于动量。

动量是力的时间积累，角动量就是力矩的时间积累。

力能改变物体的动量，力矩改变物体的角动量。

物理学就是这么对称的

要讲明白这个问题我觉得不容易，不过我回答过类似的问题。

首先我们可以把力F可以看作一种流动的东西，只不过有点特殊，因为F是一种向量，因此在规定正方向的情况下，与正方向一致的F为流入，相反为流出。

也就是说，力F流入物体m，物体m存储的动量就会变化。就像一个水池，上面在放水，下面在漏水。放水的流量为Q，漏水的流量为L，那么水池里的水量变化的速率就是H=Q-L。

所以物体m存储的动量变化率为d(mv)/dt=∑F。这个公式应该能看懂吧？就是物体m存储的动量变化率等于流入的力减去流出的力。

Ok，其实转动也是一样的，只不过力F变成了力矩M。

也就是说，物体J存储的角动量Jω的变化率，等于流入的力矩减去流出的力矩。也就是公式d(Jω)/dt=∑M。

为什么上面两个公式的原理一模一样？

最主要原因就是物体的固有状态是一定的，也就是说“质量与质量分布”其实是同一回事。质量对应力的流入流出，而质量分布对应力的分布的流入流出。而力的分布，其实就是力矩。

先说结论。力的物理意义就是使物体的平动状态发生改变。力矩的物理意义就是使物体的旋转状态发生改变。力的定义就是物体动量的改变速度，力矩的定义就是物体角动量的改变速度。

由于所有的力都可以认为是一个大系统内部的力，没有无缘无故的爱，也没有无缘无故的力，爱是相互的，力也总是相互的，所以系统的总动量和角动量总是守恒的。从一个角度说，如果要求物理规律满足时空平移和转动不变性，也就是宇宙本身没有特殊的时空点和方向，那么任何总的系统就应当自然满足动量守恒和角动量守恒。反之，如果有特殊的方向或者时空点，那么就不满足，这个时候是否也挺有意思的？特别是对于子系统，是不是会导致外力的诞生？有意思。

单个物体的运动只有平动，没有转动，其运动自由度为3。此时就没有力矩什么事了。

两个物体之间的运动自由度为6。可以分解为总体的平动和一个物体绕另一个物体的转动。而这个转动程度的大小用物理量角动量来度量，其改变速度就是力矩。对应的，平动的度量用动量，改变速度的大小是力。

至于说三个物体之间的相互运动是否会产生新的守恒量，对应于三阶微分方程的三个第一积分呢？应该是有的，我研究研究，不过三体运动是混沌系统哦，在混沌系统中找到新的守恒量应该很有意思。

总之，物体的运动形态可以分为平动和转动。力的物理意义就是使物体的平动状态发生改变。力矩的物理意义就是使物体的旋转状态发生改变。没有别的。

我画了一个三维图，写了一点东西，可能对于理解力矩有所帮助。

力矩(或动量矩)投影为什么相等？

讨论人体击打乒乓球力学原理时，常常采用球拍围绕人体垂直轴做圆周运动的简化物理模型。由于人体是一个高度复杂的生物巨系统，属于可变质点系。从理论上说，人体挥动球拍做圆周运动的力矩M采用质点系对z轴的角动量定理来分析、讨论比较合理，即Mz=∑Mzi= dLzi/dt。
质点系中每个质点i所受外力Fi（e）对z轴的力矩Mzi等于该点i对z轴上任意一点o的力矩Mi（o）在z轴上的投影。很多人对此有些疑惑，为什么点i对z轴上任意一点o的力矩Mi（o）在z轴上的投影都是相等的？要知道它们的力矩Mi（o）的大小可是千差万别的。
画了一张图，觉得对理解这一点可能会有所帮助。特在此奉献给大家。

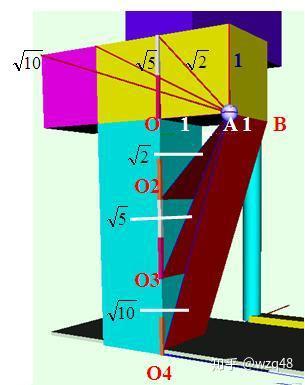
图中间立轴是z轴OO2O3O4，圆球A代表质点，OA为质点相对z轴上o点的位置矢量ri， AB是质点所受的外力Fi。为简化计算，假设它们的值均为1。 Mzi= Mi（o）= riFiSinα=1，Mi（o）的大小等于ri和Fi所成平行四边形的面积(Mi（o）= |riFiSinα|,（α是由ri转至Fi的夹角），Mi（o）方向可用右手螺旋法由ri、Fi的方向来确定。
从图中很容易看出，四个红色平面面积以及四根红色线段长度都对应着四个Mi（o）的大小，相差很大，但由于力矩方向不同，它们在 z 轴上的投影均为1。动量与角动量的投影关系与此类似。
一孔之见，仅供参考。

就是天平的力 力臂的乘积啊。

只是到力学这里写成叉乘的形式啦。

你把一本书放在桌子上，正常放吧，文具盒也行，一根手指去往前推。

手放在边长的中点，和手放在书的角的位置，你会发现，后者会发生转动。书虽然会往前，同时会扭动。因为力没有指向重心。

(这个可以通过重心是怎么得来的，推导，具体，我记得重心，就是把刚体分成很多块，每个块有质量，还有矢量，力也是矢量，运动离不开质量。所以重心的出现肯定和力之间有关系，好久没学物理了，想深入推导的自己搞下)

有转盘吗？

假设上图红圈是轴心。那么红色的力，转盘不会转动，蓝色的力，会转动我们让转盘转都是往左右拨而不是正前方推。

绿色的力，他在蓝色方向的分力，会转动，在红色方向不会转动，所以会出现F*sin（看具体给的角，有时候会是cos，主要表示的是蓝色方向会转动分力）

好了，搞清楚发生转动的力，再来看为什么会乘一个半径。这个时候，我们要用到一个常见的模型。跷跷板或者杠杆

首先看绿色的模型，我们知道，跷跷板（杠杆一个道理），要想平衡，不是两边力相等就ok了，而是f*r相等，而这里的f恰好就是让杠杆发生转动的力（当然现实中一旦跷跷板不水平，重力和力臂不垂直，就需要用和力臂垂直的分力了，这也是天平倾斜后会静止的原因自己分析）

好了，说清楚力矩了，两个相反的力矩（产生转动方向相反，一般用顺逆时针，取一个作为正方向），如果发现力矩相等，会不转动。（两个相反的力大小相等会平衡）

同样的两个力矩，他们的合力矩，（就是正负想加出现的结果）如果为正，就正方向转动，如果为负，于正方向相反的方向转动。

对比，两个相反的力→←，合力为正，正方向直线运动

这就是转动时用力矩而不是力。再来看其他问题。这个就简单了。

转动有几个量，线速度v，转动主要单位是角速度，角速度w(凑合下)v=ft/m(就是加速度乘时间)

v=w*r那么w=v/r=ft/(mr)=Mt/(mrr)好像翻车了哈哈。角速度的公式有没有等于力矩除以半径平方然后再乘其他参数的？

先了解一下刚体的加速旋转，是因为力矩的作用吧。

而这一事实实际上是由角动量守恒导致的，角动量守恒反映了空间的各向同性。